スプライン補間（Spline Interpolation）とは「スプライン関数」と呼ばれる関数を使って、金利などの情報を補間する手法のこと。

スプライン関数にはいろいろな種類があるが、金融のスプライン補間でよく使われるのは３次の自然スプライン関数と呼ばれるものである。

例えば時点 t₁，t₂，t₃ に対応する金利などのデータが３つある場合に、その中間の時点でのデータを補間したい場合、以下のような式を立てる。

　　　

は「切断べき関数」と呼ばれるもので、

　・t ＞ t₁ のとき　→　
　・t ≦ t₁ のとき　→　ゼロ

と計算する。すなわち、スプライン関数は一応形式的に１本の式の形になっているが、実際は ｔ の値によって、新たに項が付け加わっていくものである。このような式の形のおかげで、どんなにデータ数が増えてもそれを結んでいくスプライン関数が引けることになる。

また、スプライン関数はいわゆるグリッド点（上の例で言えば、 t₁，t₂，t₃ ）における微分値が連続であるから、線形補間のように、補間によってイールドカーブの傾きがジャンプするような事態を避けることができ、この結果としてそのイールイドカーブに基づくフォワード・レートのカーブも滑らかなものとすることができる。これは金利モデル等を考える際にメリットになる（下図参照）。

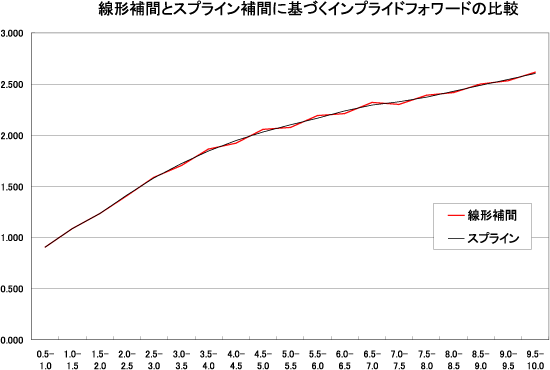
関連項目
　 線形補間

「金融エンジニアリング　キーワード解説」一覧にもどる

著作権・免責事項

• 「やさしい金融エンジニアリング講座」（以下、本解説集）の文章、図表などの著作権は、シグマベイスキャピタル株式会社に帰属しますので、複製・転載・引用・配布などは一切禁止します。
• 本解説集の利用により生じた損害はいかなる理由であれ、一切責任を負いかねますので予めご了承下さい。
• 本解説集は、予告なしに内容が変更・削除等されることがあります。
• 内容に対するご質問にはお答えすることはできませんので、ご了承下さい。