- Home >
- 金融エンジニアリング キーワード解説 >
- 連続複利
●日本FP協会 継続教育対象講座●
金融機関に頼られるシグマだからこそ、証券外務員の最短攻略法がここに!
【eラーニング】一種外務員 最短合格コース

金融エンジニアリング キーワード解説
連続複利
複利計算においては、同じ期間、同じ利率であれば複利回数が多いほど、最終的な元利合計額は大きくなる。
例えば当初元本100万円として、金利3.0%という条件の下、いろいろな複利回数で元利合計額を計算してみると以下のようになる。
| 複利計算 | 1年間の複利計算回数 | 1年後の元利合計額 |
|---|---|---|
| 1年複利 | 1 回 | 1,030,000 円 |
| 半年複利 | 2 回 | 1,030,225 円 |
| 3ヶ月複利 | 4 回 | 1,030,339 円 |
| 1ヶ月複利 | 12 回 | 1,030,416 円 |
| 1日複利 | 365 回 | 1,030,453 円 |
| 1秒複利 | 31,536,000 回 | 1,030,455 円 |
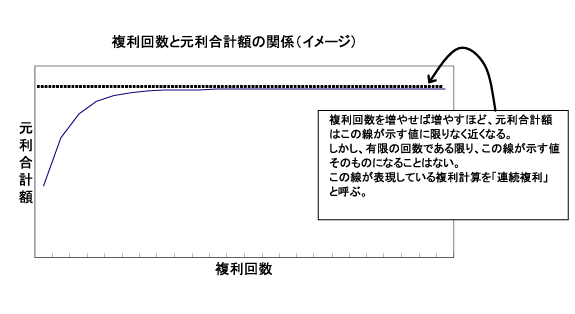
確かに、複利回数が多いほど最終的な受取元本は大きくなっているが、複利回数を増やした場合の増え方、すなわち「増える程度」は逓減している。複利回数をさらにふやして行けば増える程度はさらに小さくなって行く。実は複利回数を増やしたときの元利合計額は、青天井で増えるのではなく、ある一定の値に近づいて行く、という増え方をする。その「一定の値(複利回数がどんなに多くともある有限の数であるかぎりその値になることはないが、複利回数をふやすほどその値に近づいていく、というその値)」が示す複利のことを「連続複利(Continuous Compound)」と称する。これは言葉で言えば「限りなく」複利回数を増やした場合の複利計算であり、いいかえると「絶え間なく、連続的に」複利計算をしていく場合の複利、ということである。
期間 t 年、金利 r (ただし連続複利)で元本1円を運用した場合の元利合計額は![]() と表すことができる。
と表すことができる。
ここで使われる![]() という記号は、数学で
という記号は、数学で
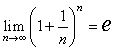
として定義される値であり、具体的には 2.71828・・ という値になる。この計算はEXCELや関数電卓などで実行できる。例えば、先ほどの例(金利3%の例)でもし連続複利だとすると、元利合計額は 1,030,454.534・・ となる。1秒複利だと 1,030,454.532・・ となるのでその値は一般的な見地からはほとんど同じである。このことは、ある当初元本が一定期間後一定の元利合計額となった場合に、適用された金利を「連続複利」として求めた場合と「1秒複利」として求めた場合とでほとんど変わりがないことを意味する。
例えば、100万円が1年後102万円になったとすれば、その金利が1秒複利であれば1.9802629%、連続複利であれば1.98902627%ということになる。ちなみに、1年複利であればもちろん2%である。このような、運用結果から連続複利ベースの金利を求める計算には「自然対数」を使えばよい。
自然対数は上の”![]() ”を「底」とする対数のことである。
”を「底」とする対数のことである。![]() という表現の代わりに一般に
という表現の代わりに一般に![]() と表記されることが多い。つまり、
と表記されることが多い。つまり、
![]()
である。
著作権・免責事項
- 「やさしい金融エンジニアリング講座」(以下、本解説集)の文章、図表などの著作権は、シグマベイスキャピタル株式会社に帰属しますので、複製・転載・引用・配布などは一切禁止します。
- 本解説集の利用により生じた損害はいかなる理由であれ、一切責任を負いかねますので予めご了承下さい。
- 本解説集は、予告なしに内容が変更・削除等されることがあります。
- 内容に対するご質問にはお答えすることはできませんので、ご了承下さい。
●日本FP協会 継続教育対象講座●
難しい数式を使わずに、日経225オプション取引の基本がわかる
【eラーニング】日経225オプション・トレーディング 初級コース





