1. はじめに

前回、債券ポートフォリオの VaR 計算をするにあたって、乱数の発生のさせ方を説明しましたので、今回はその乱数を使って実際にシミュレーションをしてみましょう。前提とする債券ポートフォリオの内容や、シミュレーションにあたっての設定などはもう繰り返しませんので、そのあたりを確認されたい方は前回までの記事をご覧ください。

　2. シミュレーションシートの説明

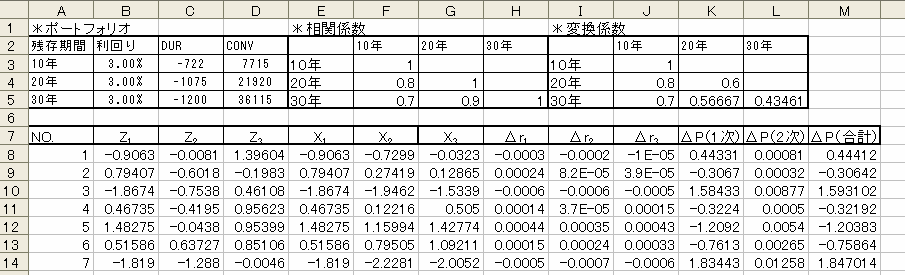
まず、前回ご紹介した手法に従ってシミュレーションをした例をご紹介しましょう。

今回のシミュレーションはこれまでと比べると大分複雑になるため、上記の図はかなり画面を縮小しています。少々見にくいですがご了承ください。

まず、 A ～ L 列の第 1 ～第 5 行のところには、ポートフォリオの債券の内容、各債券の利回り変化の相関係数、そして前回紹介した、独立の標準正規乱数から一定の相関を持つ正規乱数へ変換するときに掛け合わせる係数の値が順に入力されています（各数値については前回までの記事を参照ください）。

次に、 B ～ D 列の第 8 行以下で、独立な標準正規乱数（期待値ゼロ、標準偏差1の正規分布に従う乱数） Z1 , Z2 , Z3 を発生させます。具体的には B 、C 、 D 列の各行に乱数を 「 = NORMSINV ( RAND ( ) ) 」 で発生させます。 これを 1000 行にわたって入力し、 1000 回のシミュレーションを行います。

次に、 E ～ G 列の第 8 行以下で、一定の相関を持つ標準正規乱数 X1 , X2 , X3 にこれを変換します。このシミュレーションではここが一番難しいところだったわけですが、具体的な考え方と手法は既にご説明しました。
結論だけもう一度掲げておくと、以下の式で Z1 , Z2 , Z3 を X1 , X2 , X3 に変換すればよいのです。

［ Z1 , Z2 , Z3 を X1 , X2 , X3 に変換する式］
　
　
　

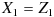
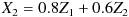
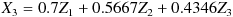
J ～ L 列の 3 ～ 5 行には、上の式で Z1 , Z2 , Z3 に掛け合わせる係数が入力されています。

次に、このようにして得られた相関を持つ標準正規乱数 X1 , X2 , X3 を 0.0003（＝ 0.03％ ）倍して、標準偏差が 0.03％ となる乱数、つまり各債券の 1 日あたり利回り変化 Δr1 , Δr2 , Δr3 に相当する乱数を作り出します。 （前述したように、 X1 , X2 , X3 間の相関係数と Δr1 , Δr2 , Δr3 間の相関係数は同じ）。
これが H ～ J 列で行っていることです。

後は、計算対象がポートフォリオになっただけで、基本的には前に債券単体でシミュレーションを行った場合とやることは同じです。

まず、Ｋ列に、デュレーション（だけ）に基づく価格変化（の近似額）を入力します。シミュレーションで得られた Δr1 , Δr2 , Δr3 の値に、各債券のデュレーション値を掛け合わせた値を足し上げます。具体的には以下のような式を入力します。
　

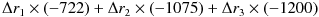
隣の L 列には、コンベクシティを利用した、デュレーションに追加する部分を計算します。
（どんな話だったか忘れたという方は本講座第 5 回を参照ください。）

具体的には以下のような式を入力します。
　

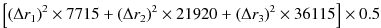
そして、 M 列には K 列と L 列を合計した値を入力します。

このようにして、 K 列にはデュレーションに基づく近似的なポートフォリオの価格変化をシミュレーションした値が、 M 列には、コンベクシティも加えたほぼ真の価格変化に近いシミュレーション値が入力されています。 ここでは 1000 行にわたって乱数を発生させていますから、再計算のたび毎に 1000 回のポートフォリオの価格変化が出力される訳です。

そして、ここでは信頼区間 99％ の VaR を計算したいので、 SMALL 関数を使って（使い方は第４回参照）、下から 10 番目の値を拾っています。それが VaR になります。