4. ＢＳ式との結果比較

さて、ここで計算したのはヨーロピアン・コールオプションの価格ですから、このようなシミュレーションをせずとも、理論的な解をＢＳ式（ブラック・ショールズ・モデル）に従い計算できます。

「ついでにＢＳ式の計算方法も知りたい！」という方もいらっしゃるかもしれませんが、計算自体は難しいものでもありませんし、本講座の目的からはそれますから、ここでＢＳ式の説明をするのは割愛させていただきます。とりあえず、このシートではＢＳ式による計算結果がセル D15 に出ていますので、シミュレーションの結果と比較してみましょう。

シミュレーション結果を表示する（クリックすると新しいウィンドウが開きます）

　　シミュレーションによる値　：　3.073
　　ＢＳ式による計算結果　：　3.061
と、かなり近い値だったことが分かります。

もちろん、シミュレーションによる計算値はシミュレーションの度ごとに変わりますので、また 10000 個の値をあらためて出力し、その平均をとれば違う結果になります。 筆者が何回か（10回ぐらい）試したところでは、最大でおよそ 0.1円 ずれていました。

このように、シミュレーションによるプライシング方法は、原理的に理論値からずれることが予想されるので、自分が今やっているシミュレーションはどのぐらいずれてしまうことがあり得るのか、ということを把握しておくことも重要です。

それを把握するためには、このようにして計算されるオプション価格の標準偏差値が分かれば、大分参考になるかと思われます。 それを計算しているのがセル D16 です。 D16 の計算式は以下のとおりです。

（３）式の 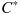とは、 J 列にずらっと並んでいる１年後のオプション価値のことを意味します。標準偏差の計算自体も J 列に並んだ 10,000 個の値そのものから計算しています。 したがって、この方法では D16 の値はシミュレーションの度ごとに変化します。 しかし、同様の計算をしてみていただければ分かりますが、この値はかなり安定しています。

この値は、およそ 0.048 のようですから 0.048／3.06 ＝ 0.0157 となり、オプションのプレミアムの 1.5％ ぐらいの標準偏差の値になります。

この標準偏差の値を小さくするには、どうしたらよいでしょうか？

答えは簡単。シミュレーションの回数を増やすことです。
ここでは一回に 10,000 個の値を出力するシミュレーションを行っていますが、 仮に一度に 10 万個の値を出力するシミュレーションであれば、（３）式の 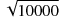が 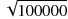に変わりますので、 標準偏差の値は 1 万回のときのおよそ 1/3 になります。