4. シミュレーション・シートのご紹介

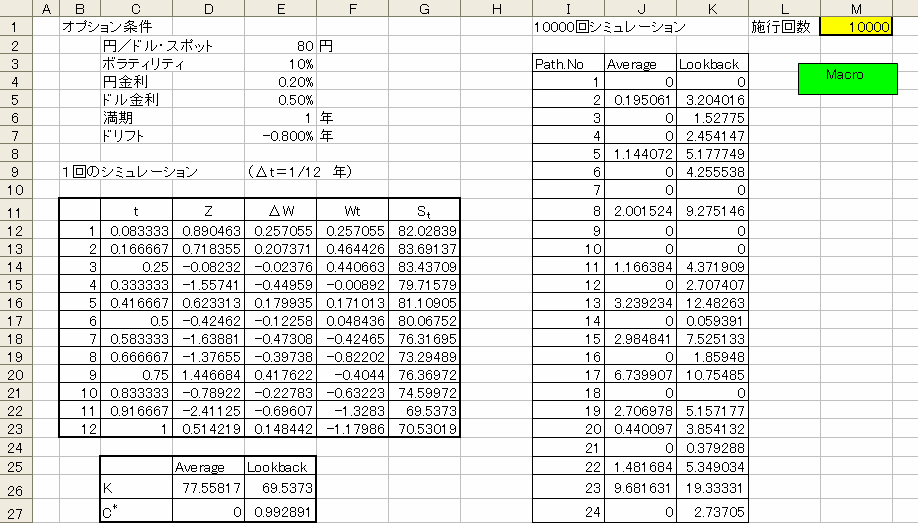
以下がシミュレーション・シートです。

ちょっとファイルが大きく、見づらくて申し訳ありません。

今回のシミュレーションで注意していただきたいポイントは、左側の中央付近に「１回のシミュレーション」と表示されている部分です。行使価格が両方のオプションともに「毎月末の為替レート」に基づいて決まる（アベレージオプションはその平均値、ルックバックオプションはその最小値）ので、ここで、１月ごとの為替レートの価格を求めています。

説明しましょう。

まず表の C 列、表題に t と表示されている部分は１月ごとの時点を表す数値が入っています。 １ヶ月は 1/12（＝0.08333） 年なので、下に１つ動くたびに、 1/12 ずつ数字が増えています。 その次の列、表題が Z となっている部分は、おなじみ「標準正規分布に従う乱数」を発生させている部分です。 ここは、前月の値などには全く関係なく値が発生します。 入力されている関数はもちろん、全ての月ともに「 = NORMSINV ( RAND ( ) ) 」 です。

その次の ΔW となっている列は、１月間でのブラウン運動の増減を示す値です。 １ヶ月ごとのブラウン運動の変動値は、すべて独立（前月の値に影響を受けない）で、期待値ゼロ、分散 1/12 の正規分布に従います。

期待値ゼロ、分散 1/12 の正規分布乱数を発生させるには、（すでに学習したように）標準正規分布に従う乱数を Z として 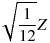という乱数を発生させればよいのです。 よって、例えば一番上の E12 のセルには 「 = D12 * (1/12) ^ 0.5 」 という式が入っています。 他のセルも同様の式が入力されています。

次の 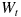という列には、毎月の ΔW の値を当該月まで加算した値が入力されています。 ここがブラウン運動そのものの動き、すなわち履歴を示す部分です。

このように計算された毎月の 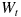の値に基づき、プレーンな通貨オプションのところでも使ったモデル式

に従い、 G 列で１月ごとの為替レートの値が計算されています。

ただし、注意しておくと、 ここでは「リスク中立経済下における期待値」を求めたいので、

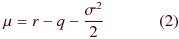
となります。
ただし、　ｒ　：　円金利、　q　：　ドル金利、　σ　：　ボラティリティ　を意味しています。

t は最初からその時点までの年数なので、 C 列に入っている数字を使います。 　具体的には、例えば２ヶ月目の為替レートを計算しているセル G13 には
　　= E$2 * EXP ( E$7 * C13 + E$3 * F13 )　
という式が入っています。
E2 は現在の為替レートの値、 E7 は「ドリフト」すなわち（２）式による μ の値、 C13 には２ヶ月間を年数で表した C 列の t の値、 E3 は「ボラティリティ」の値、 F13 が２ヶ月目での 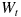の値です。