- Home >
- デュレーションってなんだろう >
- 第2回 デュレーションの基本概念 (その2)
デリバティブや投資理論の第一歩として、きっちり【金利】を勉強したい方へ!
国債投資Σ3級コース

デュレーションってなんだろう
第2回 デュレーションの基本概念 (その2)
3. 接線の「傾き」で、債券の価格変動を表す
次の図をご覧ください。
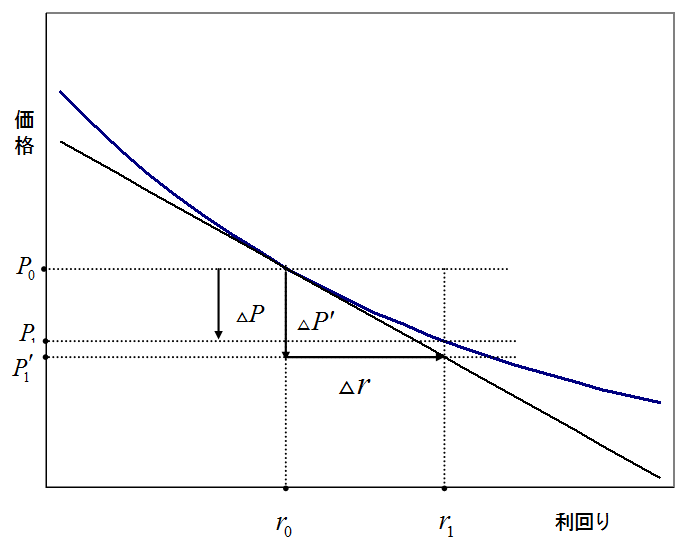
図2: 債券の利回り価格曲線と接線
太線を債券の利回り価格曲線とします。
現在の利回りは r0 であり、
債券の価格は P0です。
細線は、現在の利回り、債券価格を表す点 (r0, P0) で、債券の利回り価格曲線に引いた接線です。
この接線の「傾き」は上図の Δr, ΔP' という値により
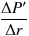 として表せることにご注意ください。
として表せることにご注意ください。
今、この債券の利回りが r0 から、 r1 に変化したとします。すると、債券価格は上図の P0 から、 P1 に変化します。
このときの利回りの変化を Δr (= r1 - r0) 、
価格変化を ΔP (= P1 - P0) とします。
ここで、債券の価格が利回り価格曲線上ではなく、実線上を変化したと仮定します。
すると、その場合は利回りが r1 に変化したときには、価格は P1 ではなく、上図の P1' になります。
このときの価格変化を ΔP' (= P1' - P0) とします。
すると、( ΔP ではなく) ΔP' の方は、接線の傾き:
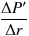 を使って以下のような形で表すことができます。
を使って以下のような形で表すことができます。

つまり、改めて言葉で表現すると、( ΔP ではなく) ΔP' ならば、「利回り変化×接線の傾き」 という式で表すことができます。
しかし、もちろん我々が最終的に知りたいのは、真の価格変化 ΔP と利回り変化 Δr の関係です。 そこで ΔP と ΔP' がどれぐらい異なるのか、ということをチェックしてみましょう。 もし、一般論として ΔP と ΔP' が「それほど」異ならない値であるならば、 ΔP についても
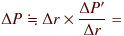 利回り変動 × 接線の傾き
利回り変動 × 接線の傾き
として「近似的な」表現が可能といえます。
著作権・免責事項
- 「やさしい金融エンジニアリング講座」(以下、本解説集)の文章、図表などの著作権は、シグマベイスキャピタル株式会社に帰属しますので、複製・転載・引用・配布などは一切禁止します。
- 本解説集の利用により生じた損害はいかなる理由であれ、一切責任を負いかねますので予めご了承下さい。
- 本解説集は、予告なしに内容が変更・削除等されることがあります。
- 内容に対するご質問にはお答えすることはできませんので、ご了承下さい。
【魅力あるキャリア、プライベートバンカー】富裕層ビジネスにおける要として・・・




