- Home >
- デュレーションってなんだろう >
- 第2回 デュレーションの基本概念 (その3)
デリバティブや投資理論の第一歩として、きっちり【金利】を勉強したい方へ!
国債投資Σ3級コース

デュレーションってなんだろう
第2回 デュレーションの基本概念 (その3)
4. 接線の傾き = デュレーション
そこで、次のグラフをご覧ください。
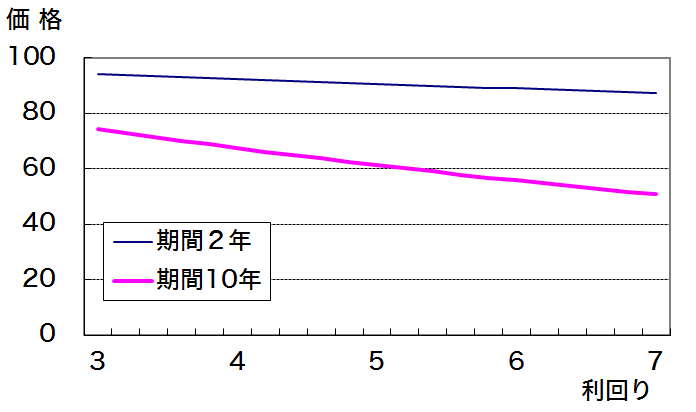
図3: 残存2年と 10 年の割引債の利回価格曲線(図1の拡大)
先ほどの図1のグラフと同じ、 2 年と 10 年、二つの割引債の利回り価格曲線ですが、違いは、横軸の利回りの変化幅のとり方です。先ほどは利回りの変化幅を 0% ~ 15% まで広くとっていましたが、今回のグラフでは、 3% から 7% までしかとっていません。つまり、今回のグラフは、先ほどのグラフのうち、「利回り 3% ~ 7% 」のところだけをとりだして、拡大したものになっているというわけです。
では、その形状はどうでしょう? 今回のグラフではずいぶん曲線が直線的に見えることに気づくと思います。 とくに、期間 2 年の割引債については、ぱっと見ただけではこれが直線なのか曲線なのか判然としないのではないでしょうか。
つまり、一般に債券の利回り価格曲線というものは、やや大雑把なことを承知で言えば、「利回り変化幅を大きくとらない範囲では、ほとんど直線みたいなもの」と言えるのです(下の図4をご参照ください)。
もちろん、「直線的」であっても直線ではないので、図2(前ページ)ではそれを強調するために、ずいぶんと「たわんだ」利回り価格曲線の図を用意しました。 しかし、現実の債券を考えると、比較的短期な債券の価格変動などを問題にする場合、つまり利回りの変動幅が「それほど」大きくないと想定されるような状況では、債券の利回り価格曲線と、現状の利回りで引いた接線を同一視して分析を進めても大して違いはないということです。
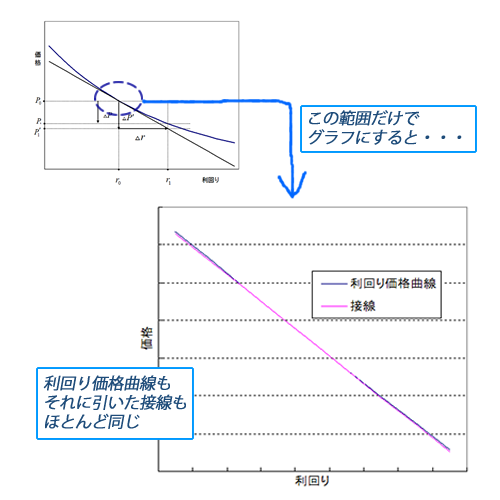
図4: 利回り価格曲線と、それに引いた接線はほとんど同じ
そして、利回り価格曲線と接線がほとんど同じと考えられるということは、先ほど問題にした「真の」価格変化 ΔP と接線上の価格変化 ΔP' もほとんど同じ値のはず、ということになります。
著作権・免責事項
- 「やさしい金融エンジニアリング講座」(以下、本解説集)の文章、図表などの著作権は、シグマベイスキャピタル株式会社に帰属しますので、複製・転載・引用・配布などは一切禁止します。
- 本解説集の利用により生じた損害はいかなる理由であれ、一切責任を負いかねますので予めご了承下さい。
- 本解説集は、予告なしに内容が変更・削除等されることがあります。
- 内容に対するご質問にはお答えすることはできませんので、ご了承下さい。
【魅力あるキャリア、プライベートバンカー】富裕層ビジネスにおける要として・・・




