コンベクシティ（Convexity）とは、デュレーションでは近似の精度が不足する場合にその精度不足を補うための概念である。

債券の利回りが Δr 変化したときの債券価格の変化 ΔP はデュレーション（ここでのデュレーションは利回り価格曲線の接線の傾きを示す）P'を使って、 と近似的に表現できる。このとき、以下のような項を付け加えると、より近似の精度が高まることが知られている（微積分学のテーラーの定理）

ここで、 P'' は、債券の利回りと価格の関係式を利回りで「２回（２階）」微分した式に現在の利回りを代入したものを示す。 この P'' がコンベクシティである（この P'' を価格 P で割ったものをコンベクシティと称する場合もある）。

コンベクシティはその求め方からわかるように、いわばデュレーション（一階微分値）を利回りで微分したものなので、利回り価格曲線のたわみが激しい債券ほどコンベクシティが大きい。よって、もし現在のデュレーションが同じでコンベクシティの異なる２債券があるとすると、コンベクシティが大きい債券の方が基本的に常に有利な価格変化をするということになる（ただし債券の利回り変化が同じ場合。下の図）

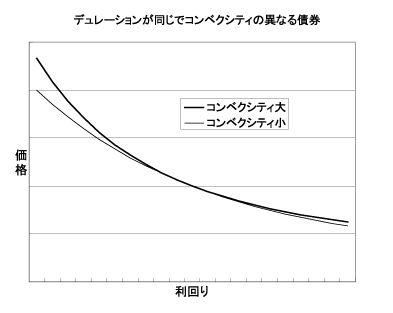
上の図のようなケースは個別債券の場合は実際は考えにくいが、ポートフォリオ単位でならば人工的に簡単に作り出すことができる。デュレーションとコンベクシティの計算式の性質上、期間の長い債券と期間の短い債券を組合わせてポートフォリオのデュレーション値をその間の期間の債券のデュレーションに合わせれば、コンベクシティは通常必ずポートフォリオの方が大きくなる。期間の短い債券と期間の長い債券を集中的に保有するいわゆる「ダンベル戦略」の理論的な根拠の一つとしてこのことが指摘されることもある。