- Home >
- エクセルを使ったモンテカルロ・シミュレーション >
- 第4回 分散共分散法によるVaRの考え方 (その1)
【証券アナリスト対策】チャレンジしたいが数学が苦手という方へ
金融数理Σ3級コース

エクセルを使ったモンテカルロ・シミュレーション
第4回 分散共分散法によるVaRの考え方 (その1)
1. はじめに
前回の設定を整理しておきましょう。
計算対象: A株(現在価格 1,000円)1株からなるポートフォリオ
VaR の内容:「保有期間 1日、信頼区間 99% 」
前提:A株の1日当たり収益率 RA は「期待値 0% 、標準偏差 2% 」の正規分布に従う
以上の設定に基づき VaR をモンテカルロ・シミュレーションで計算してみようというわけです。
2. シミュレーションの実行と結果の整理
モンテカルロ・シミュレーションのやり方は大体お分かりだと思います。前回整理したポートフォリオの損益を表す式
△P = 1,000 × RA (1)式
に基づき、△Pに該当する値を、正規乱数を発生させてシミュレーションします。10.000個の△Pを発生させてみたのが以下の表です。
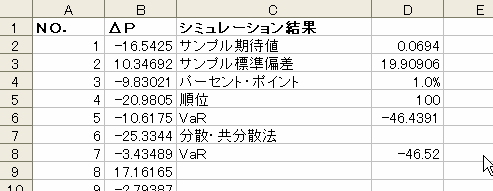
表1: エクセルでのシミュレーション結果
エクセル上で △P に該当する乱数を 10,000 回発生させた様子を表 1 に示します。 B 列の各セルにはどこも「=20×NORMSINV(RAND())」と入力されており、これが △P のシミュレーションによる実現値です。
もちろん、皆さんがご自身で作られたものと、これらの値は同じにはなりませんので注意願います(同じだったら乱数発生シミュレーションになりません)。
なお、スプレッド・シートを作成する上で、自動計算の設定になっていると、新しく入力を行うたびに 10,000 個の乱数が再発生されうっとうしいので、「ツール」メニューから「オプション」→「計算方法」を開いて、計算方法を「手動」にしておくと便利です(EXCEL2003の場合)。
ただし、この場合再計算は自動的には行われませんので、シートが完成した段階で「F9」キーを押し、シートを再計算する必要があります。
さて、次にバリュー・アット・リスクの計算ですが、それには列 B で得られた 10,000 個の値を低いものから順に並べ替え、その下から 1 パーセント目にあたる数値を調べます。「 10,000 個の値のうち、下から 1 パーセント目にあたる値」なので、 10,000×0.01=100 個目の値が該当するということにします。
この下から 100 番目の数値を求めているのがセル D6 です。
バリュー・アット・リスクでは、 1 パーセント・ポイント点を計算するという場合が多いですが、いつも 1 パーセントとは限りませんからセル D4 でそのレベルを設定できるようにしています。
セル D5 には「=10,000×D4」という式が入っており、下から何番目の値を拾えばよいかを計算しています。そして、それをセル D6 の関数の引数として使っています。
セル D6 には「=SMALL(B2:B10001,D5)」と入力されています。ここで、 SMALL とは(最初の引数)の範囲の中から、下から( 2 番目の引数)番目の値を求めるという関数で、ここではシミュレーションの結果(B2:B10001)のうちで、下から 100 番目(D5)の値を表示することになり、これが求めるバリュー・アット・リスクの値です。ここではこの値は -46.44 円となりました。
シミュレーションですから、皆さんの計算結果とぴったりとは一致していないと思いますが、だいたい同じような値が得られるはずです。
なお、セルの D2 と D3 には、今回生成した 10,000 個の △P の値の平均値(期待値)<D2>と標準偏差<D3>が計算されています。これにより、当初設定した △P の条件(期待値ゼロ、標準偏差 20 )どおりに △P が生成されていたのかを大体確認できます。
しかし、これはあくまでシミュレーションなので、時によっては当初の設定と実際に生成された △P が大分食い違っていることもあります。この例の場合は、生成された △P は概ね設定した条件通りに発生したことが分かります。
著作権・免責事項
- 「やさしい金融エンジニアリング講座」(以下、本解説集)の文章、図表などの著作権は、シグマベイスキャピタル株式会社に帰属しますので、複製・転載・引用・配布などは一切禁止します。
- 本解説集の利用により生じた損害はいかなる理由であれ、一切責任を負いかねますので予めご了承下さい。
- 本解説集は、予告なしに内容が変更・削除等されることがあります。
- 内容に対するご質問にはお答えすることはできませんので、ご了承下さい。
【魅力あるキャリア、プライベートバンカー】富裕層ビジネスにおける要として・・・




