- Home >
- エクセルを使ったモンテカルロ・シミュレーション >
- 第5回 債券の価格変化とデュレーション・コンベクシティ (その1)
【証券アナリスト対策】チャレンジしたいが数学が苦手という方へ
金融数理Σ3級コース

エクセルを使ったモンテカルロ・シミュレーション
第5回 債券の価格変化とデュレーション・コンベクシティ (その1)
1. はじめに
前回までで、モンテカルロ・シミュレーションの基礎となる正規乱数を発生させる方法の説明が終わりました。 ここからは、もう少し実務的な VaR の計算例を紹介していくことにしましょう。
銀行などで VaR を計算する対象としては、債券やスワップに代表される金利系の商品から成るポートフォリオがメインとなることが多いと思います。そこで、ここからは債券ポートフォリオの VaR 計算における利用例を見てみたいと思います。ただ、いきなりポートフォリオ単位になると話が分かりにくいと思いますので、個別債券を対象に、基本的なリスク計算の考え方についてまず説明し、次にポートフォリオのリスク計算の考え方へ展開していきたいと思います。
2. 利回り変化と債券価格変化の間の非線形性
シミュレーションが有用なケースというのは、基本的にリスク・ファクターと資産価格変化の関係が線形ではないケースが考えられます。
「関係が線形である」とは、ある変数とある変数の関係をグラフに書いたときに、1次直線の形に書けることを言います。
債券価格はその利回りが上がれば価格が下落するという関係にありますが、横軸に利回り、縦軸に価格をとってグラフにすれば、
一般的に図 1 のような形状になります。
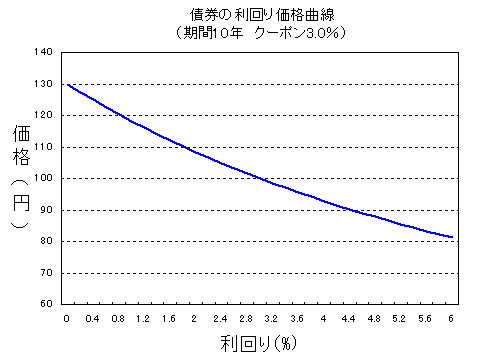
図1: 債券の利回り価格曲線
これは期間10年、クーポン3.0%の利付債の(複利)利回りと価格の関係ですが、割引債などの場合でも同様の形状、すなわち、
・右下がり
・原点方向に凸
となります。
上の2番目の性質から、債券の利回りと価格の関係は線形ではないことになります。
債券ポートフォリオのリスク管理などをする上では、債券の利回りの変化を正規分布と仮定することが多いのですが、今述べたように、債券の利回りと価格の関係は「非線形」であるため、利回りの変化が正規分布であるとき、それに基づく価格変化は正規分布にはなりません。そういわれてもピンと来ない方もおられると思いますが、正規分布というのは左右対称の分布であったことを考えていただけばイメージできると思います。
上の図 1 から、例えば現状の利回りから利回りが 1.0% 上昇した場合と、 1.0% 下落した場合の価格変化の大きさが異なることが分かります。このことから利回りの変化が左右対称な分布であっても、それに基づく債券の価格変化の分布は左右対称にはならない(つまり正規分布でない)ことがお分かりいただけると思います。
著作権・免責事項
- 「やさしい金融エンジニアリング講座」(以下、本解説集)の文章、図表などの著作権は、シグマベイスキャピタル株式会社に帰属しますので、複製・転載・引用・配布などは一切禁止します。
- 本解説集の利用により生じた損害はいかなる理由であれ、一切責任を負いかねますので予めご了承下さい。
- 本解説集は、予告なしに内容が変更・削除等されることがあります。
- 内容に対するご質問にはお答えすることはできませんので、ご了承下さい。
【魅力あるキャリア、プライベートバンカー】富裕層ビジネスにおける要として・・・




