1. はじめに

モンテカルロ・シミュレーションの利用例として、債券ポートフォリオの VaR 計算の例をご紹介しようとしていますが、前回はその準備として、デュレーションとコンベクシティ概念を使った債券価格の近似的表現方法と、実際の価格変化との関係などについてご説明しました。

今回からはシミュレーションのプロセスに入りたいと思います。

　2. シミュレーションの設定

前回までご紹介した概念や方法などを使って、債券の価格変化をシミュレーションする方法について考えてみましょう。

まず、前回も登場した期間 10 年、現在の利回り 3.0％ 、デュレーション －722 、コンベクシティ 7715 という債券の１日での価格変化をシミュレーションしてみます。

デュレーション、コンベクシティという概念は、厳密には「今この瞬間に」利回りが変化した場合の債券価格変化を捉えるための概念です。なので、 1 日という時間が経過してしまうと、厳密には前回ご紹介した（１）式や（２）式では債券価格変化を把握することはできないことになりますが、１日程度では、この点はあまり神経質になる必要はありません。

そこで、ここでは前回ご紹介した、

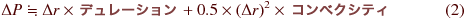
を使って、 1 日での債券価格変化を考えることにします。

なお、前回も確認したように（２）式に基づく債券価格変化は、実際の価格変化とほとんど変わりません。従って、（１）式に基づくものと（２）式に基づくものを比較すれば、（実務で多く見られる）デュレーションだけを使ったリスク管理と真の価格変化リスクとの関係も大体分かることになります。

後は前回まで紹介した手法により Δr に相当する乱数を発生させ、それに基づき（１）式と（２）式で価格変化を計算していけば良いのです。

問題は Δr の設定ですが、ここでは Δr の確率分布として正規分布を仮定し、その期待値は前回同様ゼロとします。また、標準偏差については 1 日あたり 0.03％ に設定します。これは現在の利回りを仮に 3％ とした場合、その変化率として 1 日あたり 0.03／3.0＝0.01（＝1.0％）、年率ベースでは 1.0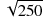％× ＝15.8％ のボラティリティに相当します。