- Home >
- エクセルを使ったモンテカルロ・シミュレーション >
- 第6回 シミュレーションによる債券 VaR (その2)
●日本FP協会 継続教育対象講座●
難しい数式を使わずに、日経225オプション取引の基本がわかる
【eラーニング】日経225オプション・トレーディング 初級コース

エクセルを使ったモンテカルロ・シミュレーション
第6回 シミュレーションによる債券 VaR (その2)
3. シミュレーションの実行と結果の整理
前ページの設定に基づき、期待値ゼロ、標準偏差 0.0003(=0.03%) の正規分布に従う乱数を発生することにより、 Δr の実現値を生成します。 Δr の実現値が得られれば、 ΔP の実現値は、(1)式及び(2)式に従って計算します。表 1 は前回と同様に 10,000 回のシミュレーションを行った例です。
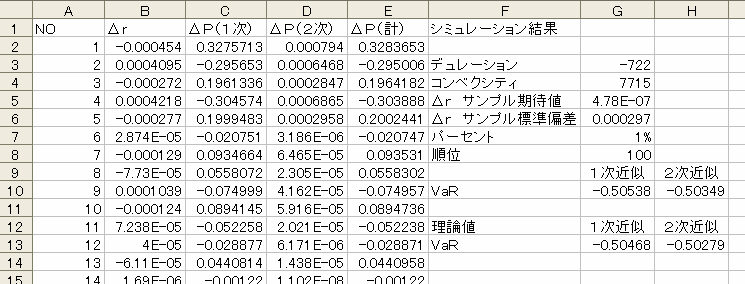
表1: シミュレーション例
B 列の各セルで Δr を生成しています、 C 列には、隣の B 列で生成した Δr に基づき、(1)式、すなわち
Δr × デュレーション
で計算した の近似額が計算されています。
D 列には、(2)式からデュレーションによる近似計算部分を除いた部分、すなわち
0.5 × (Δr)2 × コンベクシティ
の部分が入力されています。
その隣の E 列には、これら 2 つの値の合計、すなわち(2)式による ΔP の値が入力されています。
具体的には、 B 列の各セルはどれも、「=0.0003*NORMSINV(RAND())」と入力され、 C 列、 D 列については、例えばセル C2 の計算式は「=G$3*B2」、 D2 の計算式は「=0.5*G$4*B2^2」です。 C 列、 D 列の他のセルはこれらの式をコピー&ペーストすればでき上がりです。 E 列は C 列、 D 列の値を足し合わせています(例えばセル E2 では「=C2+D2」)。
なお、シート作成時には前回と同様に「計算方法」は「手動」設定にしておくことをお勧めします(設定方法は第4回参照)。
第4回と同様な方法でシミュレーションした結果を G 列~ H 列に表示します。それぞれのセルに入力されている数式と意味は、以下の通りです。
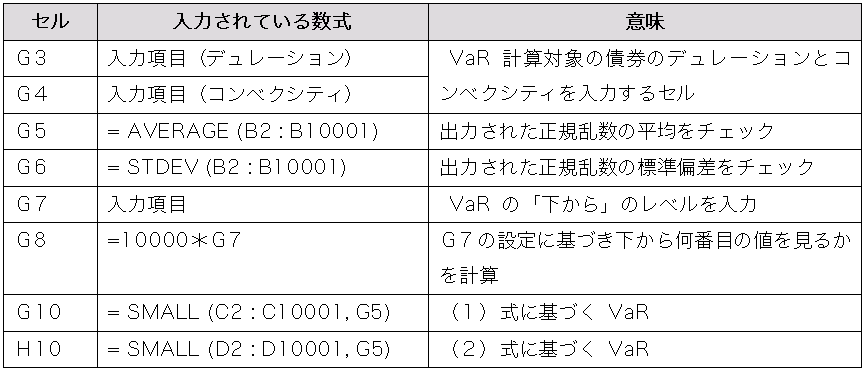
信頼区間 99% の VaR を計算するセルは G10 と H10 で、 10,000 回のシミュレーションのうち下から 100 (セル G8 の値)個目を VaR として採用するために、「SMALL」という関数を用いています(既にご説明しました)。ここではシミュレーションの結果として、(1)式、すなわちデュレーション概念による近似的な価格変化表現に基づく VaR が -0.5054 円、(2)式に基づく VaR が -0.5035 円となりました。
もちろんシミュレーションですから、結果は計算の度に異なり、皆さんの計算結果とは必ずしも一致しませんが、似たような値が得られるはずです。
著作権・免責事項
- 「やさしい金融エンジニアリング講座」(以下、本解説集)の文章、図表などの著作権は、シグマベイスキャピタル株式会社に帰属しますので、複製・転載・引用・配布などは一切禁止します。
- 本解説集の利用により生じた損害はいかなる理由であれ、一切責任を負いかねますので予めご了承下さい。
- 本解説集は、予告なしに内容が変更・削除等されることがあります。
- 内容に対するご質問にはお答えすることはできませんので、ご了承下さい。
【魅力あるキャリア、プライベートバンカー】いつかは目指したい、信頼の証。




