- Home >
- エクセルを使ったモンテカルロ・シミュレーション >
- 第6回 シミュレーションによる債券 VaR (その3)
●日本FP協会 継続教育対象講座●
難しい数式を使わずに、日経225オプション取引の基本がわかる
【eラーニング】日経225オプション・トレーディング 初級コース

エクセルを使ったモンテカルロ・シミュレーション
第6回 シミュレーションによる債券 VaR (その3)
4. 1次近似と2次近似の比較
前ページのシミュレーションでは、 1 次近似<(1)式による近似>による VaR と、 2 次近似<(2)式による近似>による VaR を比較してみると、この場合およそ 0.002 円ぐらいの違いになりました。この違いもシミュレーションの度に変わりますが、概ねその違いは大きくないはずです。
デュレーションの説明で、一般的な債券で利回りがそれほど大きくないならば、デュレーションの近似と真の価格変化の差は大きくないということを申し上げましたが、 VaR の計算でもそのことが反映しているわけです。
しかし、以上の結果から、債券の価格変化はデュレーションを使った近似的な把握で十分であると結論づけるのは、やや早計です。 デュレーションについて簡単にご説明したときに、 2 年と 10 年の割引債の利回りと価格の関係を示すグラフを見ていただきましたが、 10 年債の方がより「たわんでいた」ことを思い出してください。一般に、債券は残存期間が長いものほど、利回りと価格の関係を示すグラフはたわみが激しくなります。
デュレーションというのは、(これまた前述したように)、利回りと価格の関係を直線と仮定した場合の価格変化を捉えるための概念ですから、利回りと価格の関係を示すグラフのたわみが大きいほど、デュレーションに基づき考えた価格変化と実際の価格変化はズレてしまいます。
従って、一般論として、残存期間が長い債券ほど、(1)式(すなわち、デュレーションのみを使って価格変化を認識した場合)と(2)式で捉えた債券価格変化のズレが大きくなります。
そこで、期間 30 年の割引債というものがあるとして、同じシミュレーションをして見ましょう。現在の利回りが 3.0% とすると、デュレーション値は -1200 、コンベクシティは 36115 となります。
1 日あたりの利回り変化の標準偏差をやはり 0.03 %として、先ほどと同様のシミュレーションをした結果が下表です。
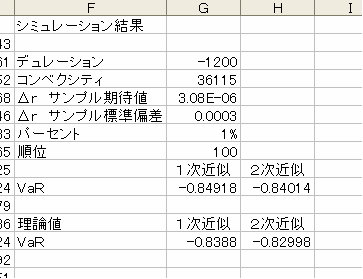
表2: 30年債でのシミュレーション結果
(1)式に基づく VaR と(2)式に基づく VaR の違いは、約 0.01 円になりました。もちろん、やはりこの値もシミュレーションの度に変わりますが、先ほどは 0.002 円でしたから、違いが大分大きくなったことはイメージしていただけると思います。
著作権・免責事項
- 「やさしい金融エンジニアリング講座」(以下、本解説集)の文章、図表などの著作権は、シグマベイスキャピタル株式会社に帰属しますので、複製・転載・引用・配布などは一切禁止します。
- 本解説集の利用により生じた損害はいかなる理由であれ、一切責任を負いかねますので予めご了承下さい。
- 本解説集は、予告なしに内容が変更・削除等されることがあります。
- 内容に対するご質問にはお答えすることはできませんので、ご了承下さい。
【魅力あるキャリア、プライベートバンカー】いつかは目指したい、信頼の証。




