- Home >
- エクセルを使ったモンテカルロ・シミュレーション >
- 第7回 相関を持った乱数発生(1) (その1)
●日本FP協会 継続教育対象講座●
難しい数式を使わずに、日経225オプション取引の基本がわかる
【eラーニング】日経225オプション・トレーディング 初級コース

エクセルを使ったモンテカルロ・シミュレーション
第7回 相関を持った乱数発生(1) (その1)
1. はじめに
ここまで、モンテカルロ・シミュレーションを実行するために、基礎知識として知っておかねばならないことを説明してきました。ここからは、より実務的なシミュレーションの利用例をご紹介していきたいと思います。まず、債券ポートフォリオの VaR 計算例について見ていきます。
ただし、何回か申し上げているように、モンテカルロ・シミュレーションが有用なケースというのは基本的に状況が複雑なケースであり、説明が難しいものになります。そこで、今までに増して、理論的な部分では省略が多くなることを予めお断りしておきます。
今回、次回あたりで説明する内容を理解するのに必要な数理は基本的な統計学の本などを開けば大抵出てきますし、あるいは、
シグマインベストメントスクール 通信教育「金融数理Σ3級コース」
などでも説明されていますので、理論面をもっと知りたいという方がいらっしゃったらこれらに当たってみてください。
2. 設定
前回に引き続き債券ポートフォリオの VaR (保有期間1日、信頼区間 99% )を求めることを考えてみましょう。ただし、今回は単一の債券ではなく、3つの割引債(それぞれ額面 100 円づつ)からなるポートフォリオを想定することします。
3つの割引債の残存期間、現状の利回り、デュレーション、コンベクシティの値を以下の通りとします。
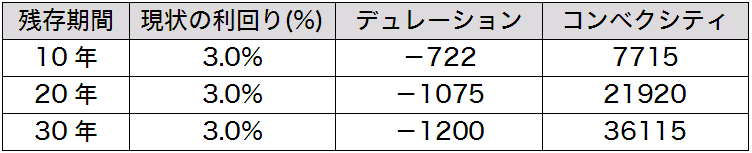
図1: ポートフォリオの内容
各債券の1日あたりの利回り変化は正規分布に従い、その標準偏差は全て 0.03% とします。また1日あたりの利回り変化の期待値はゼロとします。この辺りの設定は前回と全く同様です。
前回の最後に申し上げたように、債券の利回りと価格は一対一で対応しますので、以上の3つの債券の利回り変化が全く同じと仮定すれば、 VaR を計算するのにシミュレーションなどは全く不要です。前回までの単一債券の場合と同様、利回り変化について「上から 1% 」の値を調べ、その利回り変化に対応する3つの債券の価格変化を合計すれば 99% の VaR を簡単に計算できます。
でも、3つの債券の利回り変化が毎日全く同じということはありえないでしょう?
債券の利回りは、実務家の方はよくご存知のように確かに個別性が乏しい傾向があります。しかし、期間の異なる債券の利回り変化が毎日全く同じと仮定するのは無茶です。
そこで、今回は、3つの債券の利回り変化をそれぞれ別に発生させシミュレーションします。
3. 相関を持った乱数の発生方法
3つの債券の利回りが別々に変化するシミュレーションをすると申し上げましたが、ここで問題になってくるのが、別々に変化するとは言え、3つの債券の利回り変化の値の発生の仕方が、全くお互いに無関係であってはまずいだろう、ということです。
複数のサイコロをふったとき、サイコロの目は相互に全く何の関係もなく値をとります。しかし、現実の債券の利回り変化は、全く同じという訳ではありませんが、かなり似たような変化することが多いことはご存知の通りです。
シミュレーションをする場合には、なるべく現実に沿った形でシミュレーションしなければ意味がないですから、債券の利回り変化についてのこのあたりの特徴をうまくシミュレーションに組み入れる必要があります。
結論を申し上げると、このような特徴をシミュレーションに組み入れるには、各債券の利回り変化の相関係数の値がある設定された値になるようにシミュレーションをすれば良いと考えられます。
詳しい説明は省きますが、相関係数とは2つの確率変数間の「関係性」を示す値で、-1から1までの範囲の値をとります。相関係数が1のときは両者は常に同じ方向(片方が大きい値をとるときはもう片方も必ず大きい値をとる)に動き、相関係数が-1のときは両者は常に逆の方向に動きます。
そこで、ここでは先ほど挙げた3つの債券の1日当たりの利回り変化の相関係数が以下のようになるようにしたいと思います。
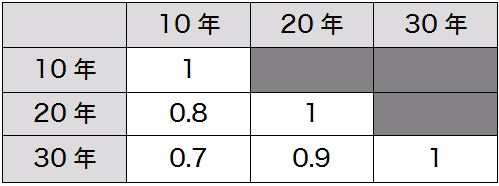
図2: 各債券の利回り変化の相関係数
例えば、 10 年債と 20 年債の利回り変化の相関係数は 0.8 、 10 年債と 30 年債の利回り変化の相関係数は 0.7 です。債券の利回りの変化の仕方は残存期間が近いものほど似たような動きになりますから、それを考慮して残存期間が近いものほど相関係数が高くなるように設定しました。
しかし、もちろんこれらの数字はあくまで仮設のもので、実際に皆さんがシミュレーションを行う場合は、標準偏差などと同様、実際の過去のデータからこれらの値を推定するという作業が必要になります。なお、マスの対角線のところにはすべて1という数字が入っていますが、これは同じものどうしの相関係数ということで、(当然全く同じ動きになりますから)相関係数は1になるわけです。
著作権・免責事項
- 「やさしい金融エンジニアリング講座」(以下、本解説集)の文章、図表などの著作権は、シグマベイスキャピタル株式会社に帰属しますので、複製・転載・引用・配布などは一切禁止します。
- 本解説集の利用により生じた損害はいかなる理由であれ、一切責任を負いかねますので予めご了承下さい。
- 本解説集は、予告なしに内容が変更・削除等されることがあります。
- 内容に対するご質問にはお答えすることはできませんので、ご了承下さい。
【魅力あるキャリア、プライベートバンカー】いつかは目指したい、信頼の証。




