3. 相関を持った乱数の発生方法（つづき）

相関係数の設定は説明しましたが、問題はここからです。

各債券の 1 日あたりの利回り変化の相関係数が、以上の値になるように、そして利回り変化の標準偏差が 0.03％ になるように（期待値はゼロ）、そして正規分布に従うように各債券の利回り変化の値を発生させたいのですが、どうしたらよいか、ということです。

この講座の趣旨やレベルから言って、この部分についてあまり原理的な話はできないのですが、こういう場合に使う定番的手法として「コレスキー分解」というものがあります。本などにも具体的な計算方法などは紹介されています。本などで紹介されている記述ではちょっと難しい感じがすると思いますが、統計学に関する基本的な知識さえあればこの場合の具体的な方法は理解できるので、ポイントだけ押さえる形で説明して行きましょう。

以下に掲げるポイントとなる定理は、基本的な統計学の知識で理解できるものばかりですが、ここではこれらの定理そのものについての説明はしません。分かりにくければ、最後の具体的な計算方法のところだけ見ていただいても結構です。

［ポイントとなる定理１］

α、βを任意の正の定数として、 X と Y の相関係数と、 αX と βY の相関係数は同じ。

このことから、一定の相関係数を持ち、それぞれ標準偏差が 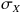、 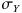である２つの乱数を作りたい場合、とりあえず、標準偏差が１で、一定の相関係数を持つ２つの乱数 X、 Y を作り、次に 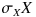、 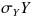として、２つの標準偏差の値を掛け合わせることで目的の乱数が作れることが分かります。

よって、ここでのポイントはどうやって一定の相関係数を持つ標準偏差が１の乱数を作り出すかです。

［ポイントとなる定理２］

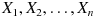が相互に独立な標準偏差が 1 の確率変数で、定数 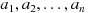が
を満たすとき、以下の式で定義される確率変数 Y の
標準偏差は 1 である。

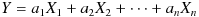
相互に「独立」な確率変数とは、簡単に言えば、サイコロをいくつか同時に振ったときの目の関係のように、お互いに相手に全く影響されずに発生すると考えられる確率変数のことを言います。独立な確率変数の相関係数はゼロになります。例えば、エクセルの２箇所にセルに RAND ( ) 関数を入力して同時に乱数を発生させれば、その２つの乱数の関係は独立になります。

［ポイントとなる定理３］

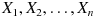が相互に独立な標準偏差が 1 の確率変数で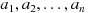、定数 及び定数
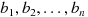がそれぞれ 、 を満たすとする。

このとき、以下の式で確率変数 Y と Z を定義する。



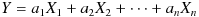
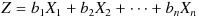
この Y と X の相関係数は以下の式で計算される。

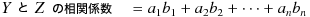
「ポイント」と言うには複雑すぎるポイントだったかもしれませんが、とりあえず以上の知識を前提とすれば、課題であった、一定の標準偏差、相互に一定の相関係数を持つ正規乱数は比較的簡単に作り出すことができます。

早速やり方をご紹介したいところですが、長くなりましたので続きは次回ということで・・・。