- Home >
- エクセルを使ったモンテカルロ・シミュレーション >
- 第8回 相関を持った乱数発生(2) (その1)
●日本FP協会 継続教育対象講座●
マーケットの動きを心理面から読み解く。
【eラーニング】「行動経済学」で学ぶ トレード心理と戦略コース

エクセルを使ったモンテカルロ・シミュレーション
第8回 相関を持った乱数発生(2) (その1)
1. はじめに
前回は、債券ポートフォリオの VaR をモンテカルロ・シミュレーションで計算してみようということで、相互に一定の相関を持つ正規乱数の発生方法について、そのための基本的な理論ポイントについてお話したところで終わりました。
今回は、具体的な乱数の発生方法について、前回お話した基本的な設定に基づき見ていきます。
2. 設定と課題の確認
状況がややこしくなっているので、もう一度ここで何をしたいかを整理しておきましょう。 VaR (保有期間1日、信頼区間 99% )を計算したい対象は以下の3つの債券(額面 100 円ずつ)からなるポートフォリオです。
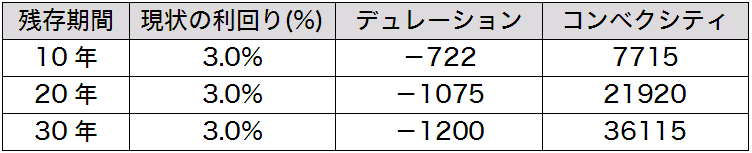
図1: ポートフォリオの内容
モンテカルロ・シミュレーションで VaR を計算するために、以上の3つの債券の1日あたりの利回り変化に該当する3つの乱数をPC上で発生させます。そのとき、3つの乱数が以下のような相関係数を持つ、標準偏差 0.03% の正規分布(期待値ゼロ)に従うようにしたいわけです。
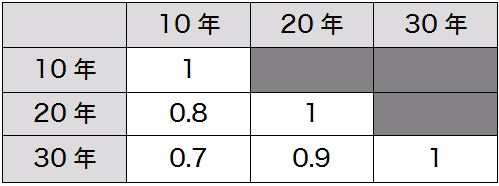
図2: 各債券の利回り変化の相関係数
で、このようなシミュレーションを行うために必要な理論ポイント3つを前回ご紹介しました。それは長くなるので再掲しません。 忘れてしまった方は前回を参照ください。
それでは具体的な方法を見ていきましょう。
3. 具体的な乱数発生方法
(1) 一定の相関を持つ標準偏差1の正規乱数
期間 10 年の債券の1日あたり利回り変化を Δr1 、 期間 20 年の債券の1日あたり利回り変化を Δr2 、 期間 30 年の債券の1日あたり利回り変化を Δr3 と表現することにします。
最終的にはこの Δr1 ~ Δr3 に相当する乱数をPC上で作り出したいわけですが、 前回の [ポイント1] で申し上げたように、確率変数 X と Y の相関係数と、確率変数 αX と βY (αとβは正の定数)の相関係数は同じですから、まず、相互に上で示した相関係数を持ち、期待値ゼロ、標準偏差が1の乱数 X1 , X2 , X3 を発生させ、 次に(標準偏差 0.03% にするために) 0.0003 を掛けて Δr1 ~ Δr3 を作り出すことにします。
つまり、まず以下のような形で Δr1 ~ Δr3 を定義します。
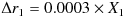
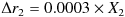
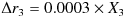
ただし、 X1 , X2 , X3
は相互に以下の相関を持つ、期待値ゼロ、標準偏差1の正規乱数とする。
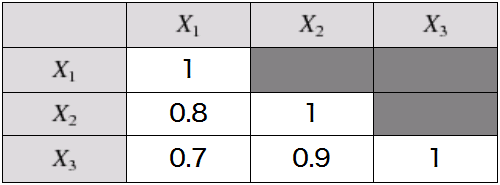
図3: X1 , X2 , X3 の相関係数(図2と基本的に同じ)
著作権・免責事項
- 「やさしい金融エンジニアリング講座」(以下、本解説集)の文章、図表などの著作権は、シグマベイスキャピタル株式会社に帰属しますので、複製・転載・引用・配布などは一切禁止します。
- 本解説集の利用により生じた損害はいかなる理由であれ、一切責任を負いかねますので予めご了承下さい。
- 本解説集は、予告なしに内容が変更・削除等されることがあります。
- 内容に対するご質問にはお答えすることはできませんので、ご了承下さい。
【魅力あるキャリア、プライベートバンカー】いつかは目指したい、信頼の証。




