- Home >
- エクセルを使ったモンテカルロ・シミュレーション >
- 第11回 前提となるモデル式の紹介 (その2)
●日本FP協会 継続教育対象講座●
相場の知恵の結晶、奥深いテクニカル分析を基礎から学ぶ!
【eラーニング】テクニカル分析 初級コース

エクセルを使ったモンテカルロ・シミュレーション
第11回 前提となるモデル式の紹介 (その2)
3. ブラウン運動について
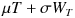 の
の
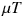 という部分は、ある定数 μ × T (オプション期間)ということで、特に申し上げるべきポイントはありません
(後から見るように、オプションプライシング上は μ を特定する必要がないからです)。
もし、次の
という部分は、ある定数 μ × T (オプション期間)ということで、特に申し上げるべきポイントはありません
(後から見るように、オプションプライシング上は μ を特定する必要がないからです)。
もし、次の
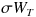 という部分が無ければ、先ほど説明したイメージ的な理解であれば
という部分が無ければ、先ほど説明したイメージ的な理解であれば
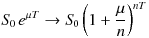
ということになります。
つまり、原資産価格がある複利ベースの収益率 μ で、時点 T まで増えていくというイメージになります。
ところが(1)式には
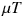 の後に
の後に
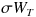 という値がくっついています。これが曲者です。
という値がくっついています。これが曲者です。
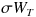 の σ は、いわゆるオプションの「ボラティリティ」の値が入ります。
ボラティリティとは原資産の価格のばらつきの大きさを表す値で、
より具体的には、原資産の収益率の年率ベースの標準偏差の値になります。
の σ は、いわゆるオプションの「ボラティリティ」の値が入ります。
ボラティリティとは原資産の価格のばらつきの大きさを表す値で、
より具体的には、原資産の収益率の年率ベースの標準偏差の値になります。
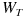 はブラウン運動に従い値をとる確率変数の時点 T における値を示しています。
と言っても「何だそりゃ」という方が多いと思います。
はブラウン運動に従い値をとる確率変数の時点 T における値を示しています。
と言っても「何だそりゃ」という方が多いと思います。
ブラウン運動という言葉は昔、理科の授業か何かで学んだ方が多いと思います。 水に浮かんだ微粒子などが不規則に動くその動きを意味しているとかいった話ですが、 ここでは、あくまで数学で定義されたブラウン運動というものに従い値をとる確率変数を意味します。
ではそのブラウン運動の数学上の定義ですが、正確なことを知りたい方は関係書などを見ていただくとして、ここではポイントとなる点だけざっと申し上げておきます。
ブラウン運動
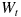 とは・・・
とは・・・
- 時点ゼロ(現時点)の値はゼロ
(すなわち
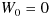 )
) - 任意の時点 s から任意の時点 t (ただし s > t )の間の増減
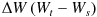 は、「期待値ゼロ、分散 t-s 」の正規分布に従う。
は、「期待値ゼロ、分散 t-s 」の正規分布に従う。 - 任意の時点
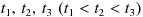 について、時点
t1
から時点
t2
までのブラウン運動の増減量
について、時点
t1
から時点
t2
までのブラウン運動の増減量
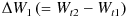 と、時点
t2
から時点
t3
までのブラウン運動の増減量
と、時点
t2
から時点
t3
までのブラウン運動の増減量
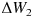 は独立である。
は独立である。
以上のような性質を満たして、時間の推移に伴いさまざまな値をとる確率変数のことを言います。
といっても、このような値をうまくイメージできるかというとちょっと難しいと思います。 統計学上のブラウン運動とは、あくまで数学上の概念であって、現実的な存在ではないからです。
もともと、オプション・プライシングなどで使う「モデル」とはあくまで「モデル」であって、現実の金融商品の価格変化と「何となく整合しそうな」数学的な表現ということに過ぎません。決して現実そのものではありません。
(では、なぜそんなモデルを使うのかと思われる方もいるかもしれませんが、その説明はここではできないのでまたの機会に・・)
従って、開き直ってしまえば、イメージが湧こうが湧くまいがこのモデル式に従って計算ができればよいのです。
で、具体的に計算をする観点から言うと、以後の説明で重要なのは、時点 0 から始まるブラウン運動が、時間 t 経過したときの値
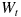 が、どんな確率分布になるかを把握しておくことです。
が、どんな確率分布になるかを把握しておくことです。
それは、上のブラウン運動の性質より「期待値 0 、分散 t の正規分布」になります。
正規分布に従う乱数の発生のさせ方はもうすでに何回か出てきましたし、 er という値は EXCEL では「 EXP(r) 」として簡単に計算できます。 従って、(1)式に基づいて、オプションの原資産価格推移のシミュレーションをすることが可能です。
大分方向性が見えてきたことと思いますが、長くなりましたので続きは次回ということで・・・。
著作権・免責事項
- 「やさしい金融エンジニアリング講座」(以下、本解説集)の文章、図表などの著作権は、シグマベイスキャピタル株式会社に帰属しますので、複製・転載・引用・配布などは一切禁止します。
- 本解説集の利用により生じた損害はいかなる理由であれ、一切責任を負いかねますので予めご了承下さい。
- 本解説集は、予告なしに内容が変更・削除等されることがあります。
- 内容に対するご質問にはお答えすることはできませんので、ご了承下さい。
【シグマインベストメントスクール】ならでは、タイムリーで深い実務的な知識が学べる・・・




