3. ここまでの話の整理と課題

さて、プライシング対象の商品も設定しましたので、早速「いざシミュレーション！」といきたいところですが、残念ながらここまでの知識だけではオプションのプライシングは難しいと思います。 この後、ちょっと分かりにくい話をする必要があるので、その前に、ここで行うとしているプライシングの基本的考え方をもう一度整理しておきましょう。

ここで実行しようとしているオプション・プライシングの前提となる基本的な考え方は、「『デリバティブ商品の価格は、リスク中立経済下における当該デリバティブ商品の将来価値の期待値』の現在価値」として求められる」というものです。

ここでの評価対象は、ドル円為替レートを対象にしたコール・オプションですから、満期時点においてはコール・オプションの価値は、

として決まります。

よって、前回ご紹介したモデル式

に従って、ドル円為替レートが変化すると仮定した上で、リスク中立経済下における（１）式の値の期待値を求め、それを現在価値にすればよいわけです。

しかし、ここまでリスク中立経済とはどんなものかという説明はしましたが、具体的にどうやったらリスク中立経済下における期待値が求められるか、ということはお話していません。この部分がオプション・プライシング上の非常に重要なキモの部分です。

では、次にその点についてご説明しましょう。

　4. リスク中立経済下における期待値

リスク中立経済下における期待値を考えるポイントは、前々回リスク中立経済について説明したときに述べた「リスク中立経済においては金融商品のリターンの期待値はリスクフリーレートと同じ」という点にあります。

したがって、オプション満期までの期間に対応するリスクフリーレートを r （ただし連続複利ベース）とすると、 時点 T における金融商品の価格を ST としたとき、そのリスク中立経済下における期待値 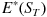（Ｅの右肩についている ＊ は「リスク中立経済下における期待値」を示す特殊表現） は以下の値でなければなりません。
　

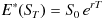
ところで、（２）式 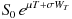に従ってその期待値を計算すると、その期待値は
　
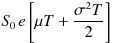
となります（何故かを知りたい方は統計学の本で「対数正規分布」について調べてみてください）。
（注）［　］の部分は e の「指数」にあたり、本来は e の右肩に載せて表記するべきものですが、 あまりにも見ずらくなってしまうのでこのような表現としています。

よって
　
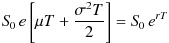
となるように、（２）式の μ を決めてやり、その μ に基づいてシミュレーションをすれば良いと考えられます。そのような μ は方程式の両辺の指数部分を比較することにより
　
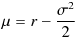
となることがわかります。

μ をこの値に設定した上で（２）式に従いシミュレーションをすれば、「リスク中立経済を前提にしたシミュレーション」を行っていることになります。