5. ちょっとややこしい話

これですぐシミュレーションができそうですが、実はここで評価しようとしているのは為替レートを対象にしたオプションであるために、さらに「ひとひねり」必要なのです。

リスク中立経済下においては、金融商品のリターンの期待値がリスクフリーレートになる必要があることから、ある金融商品 S の時点 T における価値の期待値は、以下の式を満たす必要があると申し上げました。
　

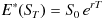
しかしこれは為替レートにはそのままあてはまらないのです。

具体的に考えてみましょう。例えば皆さんが現時点で１ドルを 80 円で購入したとします。１年後、為替レートが１ドル 90 円になっていたとすると、１年前に買ったドルの価値は 90 円でしょうか？

もし、１年前に買ったドルを何の運用もせずほっておいたならば 90 円ですが、本来なら当然運用すべきです。 ドルですからドルの金利で運用できるので、ドルの１年物金利を q とすれば、
　
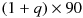
という価値になっていることになります。

金融商品の価格を理論的に考えるときは、本来運用して増やせるものは当然運用するという考え方を前提にしていますので、リスク中立経済下における１年後の為替レートの期待値は、 「現在の為替レート× er 」ではなく、今の例に準ずる形で、 （ドル金利で1年間運用した１ドルの価値×1年後の為替レート）の期待値が 「現在の為替レート× er 」になる、という形で決まります。

文章だと分かりにくいので、式で表現しましょう。

現時点でのドル円為替レートを S0 、１年後のドル円為替レートを S1 とし、１年物円金利（ただし連続複利）を r 、ドル金利を q とするとき、リスク中立経済下における S1 の期待値は、 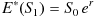ではなく、
　
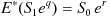
という形で決まります。すなわち、
　
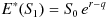
となります。

先ほどのμの決め方の話にこのことをあてはめると、
　
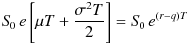
となるように、 μ を決めればよいということになります。

したがって、（２）式における μ を
　
と設定して、為替レートについてのシミュレーションを行い、
　Max（満期時為替レート － 行使価格 , 0）
の期待値を求めれば、「リスク中立経済下における為替コールオプションの価値の期待値」が求められることになります。

*　　　*　　　*　　　*　　　*

ずいぶん分かりにくい話が続きました。デリバティブやファイナンス理論についてかなり知識のある方でないと、 理解は困難な話だったかもしれません。 分かりにくかった方は、とりあえず μ の決め方の結論だけチェックしておいていただければと思います。

次回は、具体的な EXCEL でのシミュレーション例をお見せし、 BS 式の計算結果と比較してみたいと思います。