1. はじめに

モンテカルロ・シミュレーションによるオプション・プライシングの話が続いています。前回までで、為替のコールオプションの価値を求めるシミュレーションの基本的な考え方の説明はすべて終わっていますので、今回は早速シミュレーションシートの紹介から始めましょう。

　2. シミュレーション・シートのご紹介

評価対象のオプションを再掲しておきます。

ドル円通貨コール・オプション
　満期　：　１年
　現在のドル／円為替レート　：　1ドル ＝ 80 円
　行使価格　：　80 円

※前提となる金利等の条件は、以下の通りです。
　円金利　：　0.2％
　ドル金利　：　0.5％
　ボラティリティ　：　10％

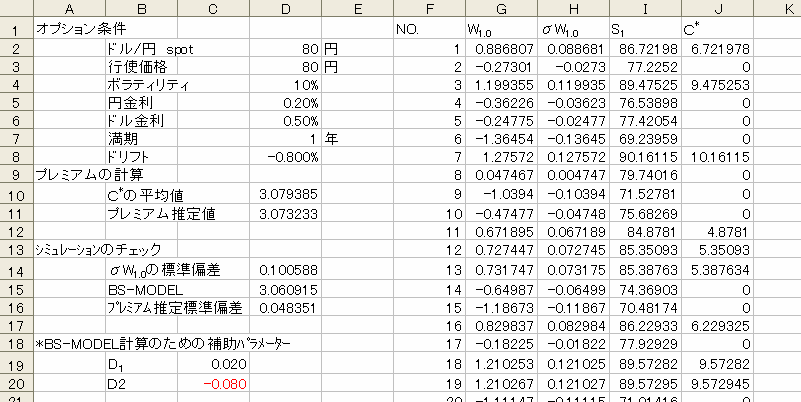
EXCEL で 10,000 回のシミュレーションを行い、オプション価値を求めたのが以下のシートです。

セル D11 のプレミアム推定値という部分が、このシミュレーションによるコール・オプションのプレミアムを計算している部分です。 3.073 円ということになります。

　3. シートの説明

シートの各部分を説明していきましょう。最初のオプション条件という部分とは、プライシング対象のオプションの条件が入力されています。

この部分の最後のドリフトというところ（セル D8 ）が重要です。これは、前回ご説明した、リスク中立確率下におけるオプション価値の期待値を求めるための μ の値が入っています。前提となるモデル式や μ を決めるための考え方などは、前回の記事をご参照ください。

具体的なμの計算式だけ述べておくと、

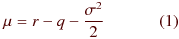
となります。
ただし、　ｒ　：　円金利、　q　：　ドル金利、　σ　：　ボラティリティ　を意味しています。
金利はいずれも「連続複利」ベースの金利を使います（現実的には、満期までの期間に対応する通常の円金利やドル金利をそのまま使っても大差ありません）。

この式で計算される μ を使って、１年後のドル円為替レート： S1 の値を、以下の（２）式で算出しているのが I 列の部分です。

S0 とは現在のドル円為替レートのことです。この式の T とは（年単位の）オプション満期までの期間を意味しますが、ここでは満期が１年なので、以後、明示的に計算に入れる必要はありません。 （２）式で１年後のドル円為替レートを計算するためには、 という値を入力しなければなりません。

この値についてはすでにかなり説明しました。 この問題においては、１年後のブラウン運動の値を意味します。１年後のブラウン運動の値は（以前説明したように）「期待値ゼロ、標準偏差１」の正規分布に従います。 よって、（２）式の値は の値次第で様々な値をとるわけです。そして、そのさまざな１年後の為替レートの値に基づき、さまざまな１年後のオプション価値になるわけです。

「期待値ゼロ、標準偏差１（＝標準正規分布）」の正規分布の値の発生のさせ方は、もうすでにこの講座で散々出てきたので説明は不要でしょう。「 = NORMSINV ( RAND ( ) ) 」 とセルに打ち込んでやれば、このような正規分布に従う確率変数値が出力されます。

このシートでは G 列にこの関数が入力されており、さまざまな 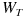の値が出力されるようになっています。 次に、この 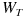の値にボラティリティ（ここでは 0.1 ＝ 10％ ）を掛けあわせたものが次ぎ H 列に、そして（２）式により１年後の為替レートを計算したものが I 列に表示されています。

具体的な計算方法ですが、 er という計算は EXCEL では「 = exp ( r ) 」 とすれば計算できるので、例えばセル I2 には「 = D$2 * EXP ( D$8 + H2 ) 」 という式が入っています。

そして、 I 列の為替レートに応じた１年後のオプション価値の値が J 列に計算されています。

リスク中立確率を使ったプライシングの原理、すなわち「『リスク中立確率下におけるデリバティブの将来価値の期待値』の現在価値」がデリバティブの価格ですから、 J 列の平均値をとって、それを金利で割り引けばデリバティブの価格になります。

ここでは、 J 列に 10,000 個のオプション価値が出力されています。 この J 列の平均値を計算しているのがセル D10 、そしてそれを１年の金利で割り引いて（ただしここでは連続複利の金利で割り引いている）オプションの価値を求めているのがセル D11 です。