●日本FP協会継続教育対象講座●　債券の基礎から実務まで、誰もが知っておきたい内容を２時間で！
【eラーニング】２時間で分かる債券の基礎コース

金融エンジニアリング　キーワード解説

β値

一般に、個々の証券のリターンと市場全体のリターンとの関係を単回帰分析（１次式の形）で考えたときの回帰係数（回帰直線の傾き）のことを言う。

例えば2005年12月から2008年3月までの月次のTOPIXのリターン（変動率）とソニーのリターンを、横軸にTOPIXのリターン、縦軸にソニーのリターンをとって、散布図の形で表すと以下のようになる。

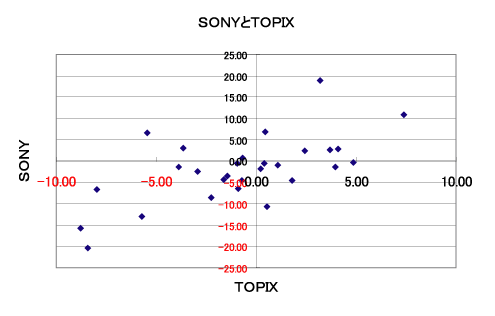
ソニーのリターンを R_S 、TOPIXのリターンを R_T として、本来ソニーとTOPIXのリターンの間には

　　　
（いわゆる市場モデルの考え方。「市場モデル」については同項目参照のこと）

という関係があるはず、とする。このとき、上のデータから β_S および α_S を「回帰分析」の最小２乗法に基づき推定すると

　　　β_S ＝1.217
　　　α_S ＝－0.973

となる。グラフ上にこの「回帰直線」を書き込むと

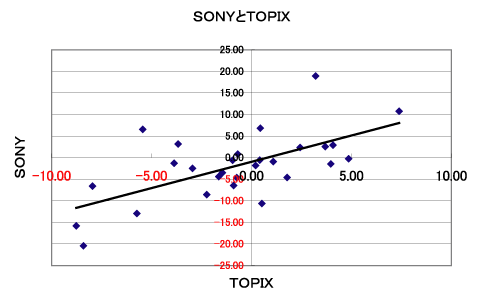
となる。この直線の「傾き」が1.217であり、いわゆるβ値である。

現代ポートフォリオ理論の文脈から言えば、β値が大きいということは証券の実質的なリスクが大きいことを意味し、CAPMでは証券の期待超過リターン（リターン－安全資産リターン　の期待値）はβ値の大きさに比例することになる。

関連項目
　市場モデル
　 CAPM

「やさしい金融エンジニアリング講座」（以下、本解説集）の文章、図表などの著作権は、シグマベイスキャピタル株式会社に帰属しますので、複製・転載・引用・配布などは一切禁止します。
本解説集の利用により生じた損害はいかなる理由であれ、一切責任を負いかねますので予めご了承下さい。
本解説集は、予告なしに内容が変更・削除等されることがあります。
内容に対するご質問にはお答えすることはできませんので、ご了承下さい。

●日本FP協会継続教育対象講座●　企業価値・ROE重視時代の株式投資に必要な企業分析を学ぶ！
【eラーニング】ファンダメンタル分析初級コース