- Home >
- エクセルを使ったモンテカルロ・シミュレーション >
- 第2回 正規乱数への変換 (その1)
ネイティブ講師によるCD付属で、英文マーケットニュースが理解できる
【eラーニング】英語で学ぶ金融基礎知識コース

エクセルを使ったモンテカルロ・シミュレーション
第2回 正規乱数への変換 (その1)
1. はじめに
前回は、シミュレーションの元になる乱数を発生させるために使う基本的な関数 RAND をご紹介しました。しかし、金融の実務でよく行うシミュレーションでは、「正規分布」と呼ばれる確率分布に従う乱数を使うことが多いのです。そこで今回は、RAND 関数による一様乱数を使って、正規分布する乱数に変える方法についてご紹介しましょう。
2. 標準正規乱数の作成
金融分野で最もよく使われる分布は何と言っても正規分布です。本当にその仮定が正しいかどうかは別として、様々な資産価格、金利などの変化あるいはリターン(変化率)が正規分布に従うものとして多くの理論が構築されています。一様乱数から正規乱数を作成する方法は先のサイコロの例ほど簡単には行きません。ただし、ここでは難しい数式展開をすることが目的ではありませんから、イメージを掴んでいただけるよう解説したいと思います。
正規分布とは何かということを厳密に解説するとなると、数学の教科書のようになってしまいますので、ここではまず、図1に示す、山のような左右対称な形をした分布だというイメージで捉えて下さい。
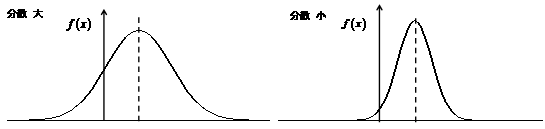
図1:正規分布
分布の中心に行くほど確率が高くなっており、ちょうど中心、すなわち山の頂上が期待値を表します。また裾野の広がり具合が分散あるいは標準偏差を表します。分布の中心すなわち期待値はいろんな値があり得ますし、据野の広がり具合も狭いものから広いものまで千差万別のものがあり得ますので、一口に正規分布といっても、その期待値と分散、標準偏差の組み合わせには無数のパターンがあります。
そこで、それらのなかで、一つだけ「標準」といえるものを定めようということで名付けられたのが「標準正規分布」で、期待値がゼロ、分散(標準偏差)が1の正規分布のことを言います。
標準正規分布に従う確率変数がある値 d 以下の値をとる確率を N(d) と表します。 N(d) は d が極めて小さい値(-∞)のときにはゼロに近づきますし、極めて大きい値(+∞)のときには 1 に近づきます(正規分布のとりえる値の範囲はどんな正規分布でも -∞~+∞ です)。
また標準正規分布の分布の中心は 0 で、それを挟んで左右対称ですから、 0 より小さい値をとる確率も、大きい値をとる確率も同じ 0.5 です。つまり、 N(0)=0.5 です。
エクセルでは、 N(d) は「=NORMSDIST( )」という関数で計算できます。( )内には d の値を入れます。良く使われる値としては「=NORMSDIST(-1.64)」の 0.05 、「=NORMSDIST(-1.96)」の 0.025 や「=NORMSDIST(-2.326)」の 0.01 (約1%)などがあります。これらの意味はバリュー・アット・リスクのところで詳しく説明します。
なお、 N(d) は確率を示す値ですから、ゼロ以下の値や 1 以上の値をとることはありません。また N(d) は d の値が決まれば値が決まるものですから、数学で関数と呼ばれるものに該当します。
統計学では、この N(d) のことを「標準正規分布の累積分布関数」などと呼びます。
次に、標準正規分布に従う乱数 X を発生させることができるとして、その X に対応する N(x) を考えてみます。
すると、この値は乱数 X の値に基づきいろいろな値をとりますから、この N(x) もまた確率変数と考えることができます。
ではこの場合 N(x) という値が 0.5 以下の値をとる確率はいくらでしょうか? 少しややこしいですが、 N(x)=0.5 に対応する X は 0 であり、 X が 0 以下のときは N(x) は 0.5 以下の値をとります。標準正規分布に従う確率変数が 0 以下の値をとる確率は当然 0.5 ですから、 N(x) という値が 0.5 以下になる確率は 0.5 ですね。
では N(x) という値が 0.2 以下の値をとる確率はいくらでしょうか? ここまでの説明では N(x)=0.2 となる X が具体的にいくらになるのかは分かりませんが、 N(x) という関数そのものの性質から答えは分かります。 N(x) という値が 0.2 以下の値をとる確率は 0.2 です。よろしいでしょうか?
同様に N(x) が α 以下の値をとる確率は α です(ただし当然 0<α<1 )。これはまさに先に見た 0 以上 1 未満の値をとる一様乱数の性質と同じです。つまり、 X が標準正規分布に従う確率変数だとして、 N(x) という確率変数を新たに考えると、この N(x) は 0 以上 1 未満の値をとる一様乱数になるわけです。すなわち、このような確率変数 N(x) を作りたければ、何のことはない、先ほど紹介した RAND( ) 関数を使えばよいのです。
著作権・免責事項
- 「やさしい金融エンジニアリング講座」(以下、本解説集)の文章、図表などの著作権は、シグマベイスキャピタル株式会社に帰属しますので、複製・転載・引用・配布などは一切禁止します。
- 本解説集の利用により生じた損害はいかなる理由であれ、一切責任を負いかねますので予めご了承下さい。
- 本解説集は、予告なしに内容が変更・削除等されることがあります。
- 内容に対するご質問にはお答えすることはできませんので、ご了承下さい。
【魅力あるキャリア、プライベートバンカー】富裕層ビジネスにおける要として・・・




