- Home >
- エクセルを使ったモンテカルロ・シミュレーション >
- 第2回 正規乱数への変換 (その2)
ネイティブ講師によるCD付属で、英文マーケットニュースが理解できる
【eラーニング】英語で学ぶ金融基礎知識コース

エクセルを使ったモンテカルロ・シミュレーション
第2回 正規乱数への変換 (その2)
2. 標準正規乱数の作成(つづき)
さて、次に N(x) の逆関数を考えてみましょう。
また少しややこしいですが、 N(x)=Y とし、 Y の値に対応する X を表す関数、つまり、 N(x) の逆関数を、 N-1(y)=x と書くことにします。
例えば、N-1(0.5)=0 ですし、先ほども紹介したように、 N(-1.96)=0.025 なので、 N-1(0.025)=-1.96 となります。
EXCEL にもちゃんとこの逆関数を計算する機能があり、
この N( ) の逆関数 N-1( ) は、「=NORMSINV( )」として計算できます。
では、 RAND() で発生させた一様乱数にこの逆関数を組み合わせるとどうなるでしょうか?
つまり、「=NORMSINV(RAND())」と入力するとどんな値が返って来るのでしょうか?
標準正規分布に従う確率変数が返ってきます。
ややこしくて分かりにくいという方は以下の図をじっくり見て頭を整理してみてください。
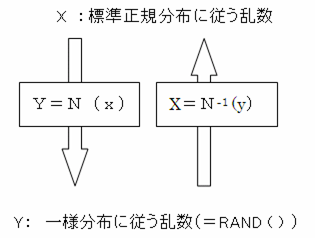
図2: 標準正規分布に従う X と一様分布 Y の関係
つまり、EXCELに「=NORMSINV(RAND( ))」と入力することにより、標準正規乱数を発生させることができるのです。
なお、この手法は正規分布に従う乱数だけでなく、その他の分布に従う乱数を作成したいときにも使うことができます。ある分布の累積分布関数の逆関数が計算できれば、NORMSINVの代わりにその逆関数を使って、目的の分布に従う乱数を一様分布から求めることができます。
この考え方は、最近リスク管理の分野等で使われる「コピュラ」という概念の中でも、その理論構成の一部として使われています。
3. 一般の正規乱数の作成
標準正規乱数から一般の正規乱数を作るのは簡単です。
結論を申し上げると、標準正規分布に従う確率変数 X が作れるとき、期待値 μ 、標準偏差 σ の正規分布に従う確率変数 Y を作りたければ
Y = μ + σX
として Y を作ればよいのです。本来は証明などが必要な話でしょうが、直観的にもイメージし易い結論なのでここではこの点については説明などは省略させていただきます。
例えば期待値が 3 で標準偏差が 0.5 の正規乱数を作りたいとしましょう。
このときは、「=NORMSINV(RAND())*0.5+3」と入力すれは良いのです。
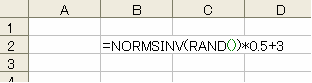
図3: 期待値 3 、標準偏差 0.5 の正規乱数の作成
こうやってどんな期待値、標準偏差の正規乱数(正規分布に従う乱数)であっても作ることができます。
次回は、この正規乱数を用い、バリュー・アット・リスクの計算に利用する方法について解説します。
著作権・免責事項
- 「やさしい金融エンジニアリング講座」(以下、本解説集)の文章、図表などの著作権は、シグマベイスキャピタル株式会社に帰属しますので、複製・転載・引用・配布などは一切禁止します。
- 本解説集の利用により生じた損害はいかなる理由であれ、一切責任を負いかねますので予めご了承下さい。
- 本解説集は、予告なしに内容が変更・削除等されることがあります。
- 内容に対するご質問にはお答えすることはできませんので、ご了承下さい。
【魅力あるキャリア、プライベートバンカー】富裕層ビジネスにおける要として・・・




