つまり、RA が 3％ であれば、 △P は 1,000×3％＝30円 というわけです。

RAが高ければ、 △P も高く、 RA が低ければ、 △P も低くなりますから、 RA について｢良い方から 99％｣の値を求め、それを 1,000 に掛け合わせれば VaR が計算できます。よって、問題は RA の確率分布を特定することになります。

実際のところ、株式の収益率（価格変化率）がどのような分布に従うかは議論のあるところなのですが、ここでは、本稿の目的上、株式の収益率は正規分布に従うと仮定します。実際このような仮定は実務でも非常によく使われます。このような、ポートフォリオの価値を変化させる要因（リスク・ファクター）が正規分布に従うという前提で VaR を計算する方法を「分散共分散法（デルタ法）」などと呼んでいます。

つまり、ここでは RA が正規分布に従うという前提で、（1）式に基づき VaR を計算します。

　4. 確率分布の具体的特定

さて、 RA が正規分布に従うというところまでは決めましたが、これだけでは VaR は計算できません。当然、期待値と標準偏差を特定する必要があります。そのために通常は過去の日次の収益率データなどに基づきこれら分布のパラメータの推定を行います。その方法についてはいくつかのバリエーションがありますが、ここでは本論からそれますので省略します。なお、2つのパラメータのうち、期待値については推定をせず、単純にゼロと置いてしまうこともよくあります。その理由は、

　(1) 期待収益率の推定値はあてにならない（精度が極めて悪い）。
　(2) 1日というような短い時間においては、収益率における期待値の影響は小さい。

といったことが収益率には一般にあてはまると考えられるからです。

そこで、ここでも期待収益率は 0％ としてしまいましょう。収益率の標準偏差は 1 日あたり 2％ （年率では、2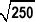％ × ＝31．6％に相当します）に設定します。このとき（1）式の関係から、資産価格変化 △P は、期待値 0 円、標準偏差 1,000×2％＝20円 の正規分布に従うことになります。
（この辺りも本来は説明が必要な部分ではありますが、話が数学に傾きすぎないよう、直観的に納得していただけそうなところは細かい説明はせず進んで行くこととします）

この確率変数（乱数）をエクセルの関数を使って実現するには、「＝20×NORMSINV（RAND（ ））」とすればよいことは前回見たとおりです。

　次回は、これらの設定を元にモンテカルロ・シミュレーションによる具体的な VaR の計算について見ていきたいと思います。